答案：A

题目分析：由二次函数的解析式可知，当x=1时，所对应的函数值y=t=a+b+1．把点（-1，0）代入y=ax²+bx+1，a-b+1=0，然后根据顶点在第一象限，可以画出草图并判断出a与b的符号，进而求出t=a+b+1的变化范围．

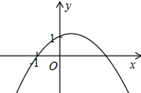
∵二次函数y=ax²+bx+1的顶点在第一象限，

且经过点（-1，0），

∴易得：a-b+1=0，a＜0，b＞0，

由a=b-1＜0得到b＜1，结合上面b＞0，所以0＜b＜1①，

由b=a+1＞0得到a＞-1，结合上面a＜0，所以-1＜a＜0②，

∴由①②得：-1＜a+b＜1，且c=1，

得到0＜a+b+1＜2，

∴0＜t＜2．

故选A．

点评：二次函数的图象与系数的关系是初中数学的重点和难点，是中考常见题，一般难度较大，需特别注意.