（1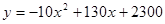），0＜x≤10且x为正整数；（2）32元；（3）定为36元或37元时，每个月可获得最大利润.最大的月利润是2720元.

题目分析：（1）根据题意知一件玩具的利润为（30+x-20）元，月销售量为（230-10x），然后根据月销售利润=一件玩具的利润×月销售量即可求出函数关系式．

（2）把y=2520时代入y=-10x²+130x+2300中，求出x的值即可．

（3）把y=-10x²+130x+2300化成顶点式，求得当x=6.5时，y有最大值，再根据0＜x≤10且x为正整数，分别计算出当x=6和x=7时y的值即可．

（1）依题意得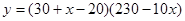        

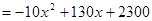
自变量x的取值范围是0＜x≤10且x为正整数；

（2）当y=2520时，得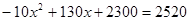（元）            

解得x₁=2，x₂=11（不合题意，舍去） 

当x=2时，30+x=32（元）

所以，每件玩具的售价定为32元时，月销售利润恰为2520元；

（3）        

∵a=-10＜0 

∴当x=6.5时，y有最大值为2722.5          

∵0＜x≤10(1≤x≤10也正确)且x为正整数

∴当x=6时，30+x=36，y=2720（元） 

当x=7时，30+x=37，y=2720（元）

所以，每件玩具的售价定为36元或37元时，每个月可获得最大利润.最大的月利润是2720元.

点评：二次函数的应用是初中数学的重点，是中考常见题，一般难度较大，需熟练掌握.