某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当未租出的车将增加1辆,每辆车的日租金每增加50元,;公司平均每日的各项支出共4800元.设公司每日租出工辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为 元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
(1)(1400-50x);(2)当日租出14辆时,租赁公司日收益最大,为5000元;(3)4辆
题目分析:(1)根据当全部未租出时,每辆租金为:400+20×50=1400(元),得出公司每日租出x辆车时,每辆车的日租金为:1400-50x;
(2)根据已知得到的二次函数关系求得日收益的最大值即可;
(3)要使租赁公司日收益不盈也不亏,即y=0,即 ,求出方程的解即可.
,求出方程的解即可.
试题解析:(1)∵某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;
当每 辆车的日租金每增加50元,未租出的车将增加1辆;
∴当全部未租出时,每辆租金为:400+20×50=1400(元),
∴公司每日租出x辆车时,每辆车的日租金为:(1400-50x);
(2)由题意得
∵-50<0,
∴该抛物线的开口方向向下,
∴该函数有最大值
当x=14时,在范围内,y有最大值5000.
∴当日租出14辆时,租赁公司日收益最大,最大值为5000元;
(3)要使租赁公司日收益不盈也不亏,即y=0.
即 ,
,
解得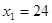 ,
,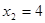 ,
,
∵x=24不合题意,舍去.
∴当日租出4辆时,租赁公司日收益不盈也不亏.