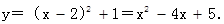问题
解答题
（1）已知二次函数y=ax2+bx+c(a≠0）的图象过A（2,0）、B（12,0），且y的最大值为50，求这个二次函数的解析式；
（2）抛物线顶点P（2,1），且过A（－1,10），求抛物线的解析式.
答案
y＝-2（x-2）（x-12）＝-2x2+28x-48；y＝（x-2）2+1＝x2-4x+5．
题目分析：（1）先根据抛物线的对称性确定顶点坐标，由于已知抛物线与x轴的两交点坐标，则可设交点式y＝a（x-2）（x-12），然后把顶点坐标代入求出a的值即可；
（2）由于已知顶点坐标，可设顶点式
，然后把A点坐标代入求出a的值即可．
试题解析：
解：（1）∵二次函数
的图象过A（2，0）、B（12，0），
∴抛物线的对称轴为直线x＝7，
∴抛物线的顶点坐标为（7，50），
设抛物线的解析式为y＝a（x-2）（x-12），
把（7，50）代入得a×5×（-5）＝50，
解得a＝-2，
∴二次函数的解析式为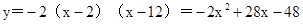
；
（2）设抛物线的解析式为y＝a（x-2）2+1，
把A（-1，10）代入得9a+1＝10，
解得a＝1，
∴