解：（1）由题意，得。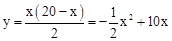

当y=48时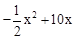，=48，解得：x₁=12，x₂=8。

∴面积为48时BC的长为12或8。

（2）∵，

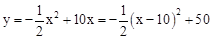∴当x=10时，y_最大=50。

（3）△ABC面积最大时，△ABC的周长存在最小的情形。理由如下：

由（2）可知△ABC的面积最大时，BC=10，BC边上的高也为10。

过点A作直线L平行于BC，作点B关于直线L的对称点B′，连接B′C 交直线L于点A′，连接A′B，AB′，

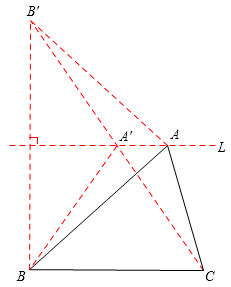
则由对称性得：A′B′=A′B，AB′=AB，

∴A′B+A′C=A′B′+A′C=B′C，

当点A不在线段B′C上时，则由三角形三边关系可得：

△ABC的周=AB+AC+BC=AB′+AC+BC＞B′C+BC，

当点A在线段B′C上时，即点A与A′重合，这时

△ABC的周长=AB+AC+BC=A′B′+A′C+BC=B′C+BC，

因此当点A与A′重合时，△ABC的周长最小。

这时由作法可知：BB′=20，∴。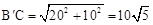

∴△ABC的周长= 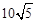+10。

因此当△ABC面积最大时，存在其周长最小的情形，最小周长为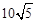+10。

题目分析：（1）先表示出BC边上的高，再根据三角形的面积公式就可以表示出表示y与x之间的函数关系式，当y=48时代入解析式就可以求出其值；

（2）将（1）的解析式转化为顶点式就可以求出最大值。

（3）由（2）可知△ABC的面积最大时，BC=10，BC边上的高也为10过点A作直线L平行于BC，作点B关于直线L的对称点B′，连接B′C 交直线L于点A′，再连接A′B，AB′，根据轴对称的性质及三角形的周长公式就可以求出周长的最小值。