问题
计算题
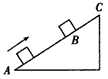
物体以一定的初速度冲上固定的光滑斜面,到达斜面最高点C时速度恰好为零,如图所示,已知物体运动到斜面长度3/4处的B点时,所用时间为t,求物体从B滑到C所用的时间。
答案
解法一:逆向思维法
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面,故
xBC=atBC2/2,xAC=a(t+tBC)2/2,又xBC=xAC/4,解得tBC=t
解法二:比例法
对于初速度为零的匀变速直线运动,在连续相等的时间里通过的位移之比为x1:x2:x3:…:xn=1:3:5:…:(2n-1)
现有xBC:xBA=(xAC/4):(3xAC/4) =1:3
通过xAB的时间为t,故通过xBC的时间tBC=t
解法三:中间时刻速度法
利用推论:中间时刻的瞬时速度等于这段位移的平均速度vAC=(vA+vC)/2=(v0+0)/2=v0/2
又v02=2axAC,vB2=2axBC,xBC=xAC/4
由以上各式解得vB=v0/2
可以看出vB正好等于AC段的平均速度,因此B点是时间中点的位置,因此有tBC=t
解法四:图象法
利用相似三角形面积之比等于对应边平方比的方法,作出v-t图象,如图所示
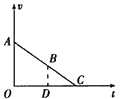
S△AOC/S△BDC=CO2/CD2
且S△AOC=4S△BDC,OD=t,OC=t+tBC
所以4/1=(t+tBC)2/tBC2,得tBC=t
