问题
解答题
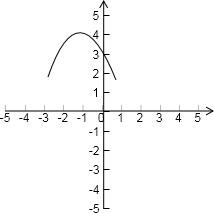
画出二次函数y=-x2-2x+3的图象,
(1)指出抛物线开口方向、对称轴和顶点坐标;
(2)求出抛物线与x轴的交点坐标;
(3)当函数值y<0时,求x的取值范围.
答案
画出函数的图象如图:
(1)a=-1,开口方向向下;对称轴是x=-
=-1;b 2a
原二次函数经变形得:y=-(x+1)2+4,故顶点为(-1,4);
(2)令y=0,得x的两根为x1=1,x2=-3,
故与x轴的交点坐标:(1,0),(-3,0);
(3)令y<0,即-x2-2x+3<0,由图象求得x的取值范围:x>1或x<-3.