问题
解答题
抛物线y＝ax2＋2x＋c与其对称轴相交于点A(1，4)，与x轴正半轴交于点B.
（1）求这条抛物线的函数关系式；
（2）在抛物线对称轴上确定一点C，使△ABC是等腰三角形，求出所有点C的坐标.
答案
（1）y=－x2＋2x＋3；（2）C（1，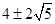
），C（1，－4），C（1，
）
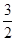题目分析：（1）根据题意知，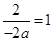
，求出a=-1.把A（1，4）代入y=-x2+2x+c,得c=3.由此可求出抛物线的解析式；
（2）分别以AB为底和腰进行讨论，从而得出结论.
试题解析：（1）由题意，点A(1，4)即为抛物线的顶点
于是抛物线的对称轴直线x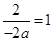＝，∴a＝－1
抛物线的解析式为y＝－(x－1)2＋4＝－x2＋2x＋3
（2）抛物线与x轴正半轴的交点B的坐标是(3，0)
若点A、B与抛物线对称轴上的点C构成等腰三角形，有三种可能：
当AB＝AC时，点C（1，）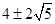
当BA＝BC时，点C（1，－4）
当CA＝CB时，点C（1，）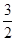
综上所述，符合要求的点C共有四个.
考点: 二次函数综合题.