问题
解答题
已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的函数解析式;
(2)求抛物线的对称轴和C点的坐标.
答案
(1)抛物线的解析式是:y=x2+2x;(2)对称轴为直线x=-1,C(-1,-1).
题目分析:(1)已知图象上的三点,求抛物线的解析式,一般都是用待定系数法,设抛物线的解析式为y=ax2+bx+c,将三个点的坐标分别带入抛物线的解析式,得到一个三元一次方程组,解这个方程组,求出系数a、b、c,从而得到抛物线解析式.(2)要求抛物线的对称轴和顶点坐标,一般地,都是将抛物线解析式配方,然后求得抛物线的对称轴和顶点.
试题解析:(6分)(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得: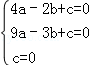 ,
,
解得: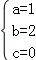 .
.
故函数解析式为:y=x2+2x.
(2)对称轴为直线x=-1,C(-1,-1).
