问题
填空题
设0<b<1+a,若关于x 的不等式(x-b)2>(ax)2的解集中的整数恰有3个,则a的取值范围是 ______.
答案
关于x 的不等式(x-b)2>(ax)2 即 (a2-1)x2+2bx-b2<0,∵0<b<1+a,
[(a+1)x-b]•[(a-1)x+b]<0 的解集中的整数恰有3个,∴a>1,
∴不等式的解集为
<x<-b a-1
<1,所以解集里 的整数是-2,-1,0 三个b a+1
∴-3≤-
<-2,b a-1
∴2<
≤3,2a-2<b≤3a-3,b a-1
∵b<1+a,
∴2a-2<1+a,
∴a<3,
综上,1<a<3,
故答案为1<a<3.

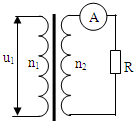
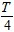 时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )
时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )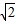
 :3
:3