某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
(1)y=30-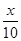 ,且0<x≤90,且x为10的正整数倍;
,且0<x≤90,且x为10的正整数倍;
(2)w=-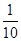 x2+20x+3000;
x2+20x+3000;
(3)一天订住21个房间时,宾馆每天利润最大,最大利润为3990元.
题目分析:(1)理解每个房间的房价每增加x元,则减少房间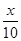 间,则可以得到y与x之间的关系;
间,则可以得到y与x之间的关系;
(2)每个房间订住后每间的利润是房价减去20元,每间的利润与所订的房间数的积就是利润;
(3)求出二次函数的对称轴,根据二次函数的增减性以及x的范围即可求解.
(1)由题意得:
y=30-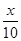 ,且0<x≤90,且x为10的正整数倍;
,且0<x≤90,且x为10的正整数倍;
(2)w=(120-20+x)(30-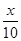 ),
),
整理,得w=-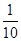 x2+20x+3000.
x2+20x+3000.
(3)w=-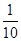 x2+20x+3000
x2+20x+3000
=-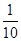 (x-100)2+4000.
(x-100)2+4000.
∵a=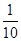 ,
,
∴抛物线的开口向下,当x<100时,w随x的增大而增大,又0<x≤90,因而当x=90时,利润最大,此时一天订住的房间数是:30-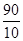 =21间,最大利润是3990元.
=21间,最大利润是3990元.
答:一天订住21个房间时,宾馆每天利润最大,最大利润为3990元.
