问题
解答题
已知二次函数y=a(x-m)2-2a(x-m)（a,m为常数，且a≠0）.
（1）求证：不论a与m为何值，该函数的图象与x轴总有两个公共点；
（2）设该函数的图象的顶点为C，与x轴交于A，B两点，当△ABC是等腰直角三角形时，求a的值．
答案
（1）见解析；（2）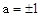
.
题目分析：(1)二次函数和x轴有两个交点，判别式>0即可；
（2）先求出顶点坐标，由△ABC是等腰直角三角形，可以得出AB边上高等于1，即可得出a的值.
试题解析：
（1）证明：y=a(x-m)2-2a(x-m)=ax2-(2am+2a)x+am2+2am
当a≠0时,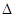
=（2am+2a）2-4a(am2+2am)
∵
∴
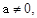
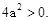
∴不论a与m为何值，该函数的图象与x轴总有两个公共点．
（2）y=a(x-m)2-2a(x-m)=a(x-m-1)2-a
∴C(m+1,-a)
当y=0时，
解得x1=m，x2=m+2.
∴AB=（m+2）-m=2.
当△ABC是等腰直角三角形时，可求出AB边上高等于1．
∴
．
∴．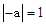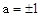