某职业学校三名学生到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
A:如果以10元/千克的价格销售,那么每天可售出300千克.
B:如果以13元/千克的价格销售,那么每天可获取利润750元.
C:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获取的利润达到600元?【利润=销售量×(销售单价-进价)】
(3)一段时间后,发现这种水果每天的销售量均不低于225千克.则此时该超市销售这种水果每天获取的最大利润是多少?
(1)y=-50x+800(x>0);(2)10或14元;(3)787.5元.
题目分析:(1)以10元/千克的价格销售,那么每天可售出300千克;以13元/千克的价格销售,那么每天可获取利润750元.就相当于直线过点(10,300),(13,150),然后列方程组解答即可.
(2)根据利润=销售量×(销售单价-进价)写出解析式,W=(-50x+800)(x-8)=600求出即可;
(3)由二次函数的性质以及利用配方法求最大值,自变量的取值范围解答这一问题.
试题解析:(1)当销售单价为13元/千克时,销售量为: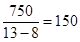 千克
千克
设y与x的函数关系式为:y=kx+b(k≠0)
把(10,300),(13,150)分别代入得:
 ,
,
解得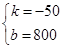 ,
,
故y与x的函数关系式为:y=-50x+800(x>0)
(2)设每天水果的利润w元,
∵利润=销售量×(销售单价-进价)
∴W=(-50x+800)(x-8)=600
0=-50(x-12)2+200
解得:x1=10,x2=14.
∴当销售单价为10或14元时,每天可获得的利润是600元.
(3)W=(-50x+800)(x-8)=-50x2+1200x-6400=-50(x-12)2+800
又∵水果每天的销售量均低于225kg,水果的进价为8元/千克,
∴-50x+800≥225,
∴x≤11.5,
∴当x=11.5时,W最大=787.5(元).
答:此时该超市销售这种水果每天获取的利润最大是787.5元.
考点: 二次函数的应用.
