若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”。
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2—4mx+2m2+1,和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2为y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的最大值。
(1)本题为开放题,答案不唯一,符合题意即可,如: ;
;
(2)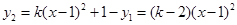 ,当
,当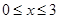 时,
时, 的最大值为20.
的最大值为20.
题目分析:(1)本题为开放题,答案不唯一,符合题意即可,如: ;
;
(2)把点A(1,1)代入函数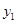 的解析式,可解得
的解析式,可解得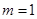 ,于是得到
,于是得到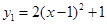 ;因为
;因为 与
与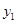 是“同簇二次函数”,可设
是“同簇二次函数”,可设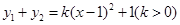 ,于是得到
,于是得到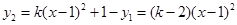 .将点(0,5)代入上式,可求得k的值,从而求得函数y2的表达式.再根据
.将点(0,5)代入上式,可求得k的值,从而求得函数y2的表达式.再根据 的函数图象即可求得当
的函数图象即可求得当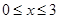 时,
时,  的最大值.
的最大值.
试题解析:(1)本题为开放题,答案不唯一,符合题意即可,如: ;
;
(2)∵函数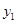 的图象经过点A(1,1),则
的图象经过点A(1,1),则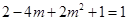 ,解得
,解得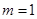 ,
,
∴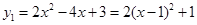 .
.
解法一:∵ 与
与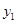 是“同簇二次函数”,∴可设
是“同簇二次函数”,∴可设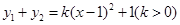 ,
,
则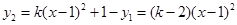 。
。
由题意可知函数 的图象经过点(0,5),则
的图象经过点(0,5),则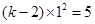 ,∴k-2=5,∴
,∴k-2=5,∴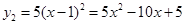 .
.
解法二:∵ 与
与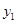 是“同簇二次函数”,
是“同簇二次函数”,
∴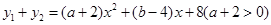 ,
,
∴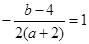 ,化简得b=-2a,
,化简得b=-2a,
又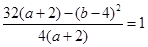 ,将
,将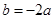 代入,解得a=5,b=-10,
代入,解得a=5,b=-10,
∴ .
.
当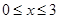 时,根据
时,根据 的函数图象可知,
的函数图象可知, 的最大值=
的最大值= .
.
