问题
填空题
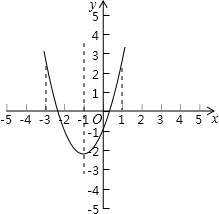
已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论:①9a-3b+c>0;②b<c;③3a+c>0,其中正确结论两个数有______个.
答案
①∵0<x1<1,
∴点(1,a+b+c)在第一象限,
又∵对称轴为直线x=-1,
∴(-3,9a-3b+c)在第二象限,故9a-3b+c>0,正确;
②∵-
=-1,∴b=2a,b 2a
∴b-a=2a-a=a>0,
又0<x1<1,抛物线开口向上,
∴抛物线与y轴交于负半轴,c<0,
∴b>a>c,不正确;
③把b=2a代入a+b+c>0得3a+c>0,正确;
故答案为2个.