问题
解答题
已知函数f(x)=loga(x+1),点P是函数y=f(x)的图象上任意一点,点P关于原点的对称点Q的轨迹是函数y=g(x)的图象。
(1)当0<a<1,解关于x的不等式:2f(x)+g(x)≥0;
(2)若当a>1,且x∈[0,1)时,总有2f(x)+g(x)≥m恒成立,求实数m的取值范围。
答案
解:由题意知,点P、Q关于原点对称,设Q(x,y)是函数y=g(x)图象上任一点,则P(-x,-y)是f(x)=loga(x+1)的图象上的点,所以-y=loga(-x+1),即g(x)= -loga(1-x)
(1)当0<a<1时,2f(x)+g(x)≥0
即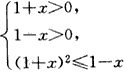
解得-1<x≤0
因此,当0<a<1时,不等式2f(x)+g(x)≥0的解集为{x|-1<x≤0};
(2)y=2f(x)+g(x)=2loga(1+x)-loga(1-x)
当a>1,且x∈[0,1)时,2f(x)+g(x)≥m恒成立,
即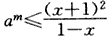 恒成立
恒成立
设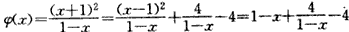
∵0≤x<1
∴0<1-x≤1
∴当1-x=1时,f(x)取最小值,φ(x)min=1
∴am≤1
∴m≤0
故实数m的取值范围是m≤0。
