问题
解答题
在同一坐标系中,画出函数y=-x2和y=-x2+1的图象,根据图象回答:
(1)抛物线y=-x2+1经过怎样的平移得到抛物线y=-x2
(2)对于函数y=-x2+1:
①当x为何值时,y随x的增大而减小?
②当x为何值时,函数y有最大值?最大值是多少?
③求y=-x2+1的图象与x轴、y轴的交点坐标.
答案
图象为:
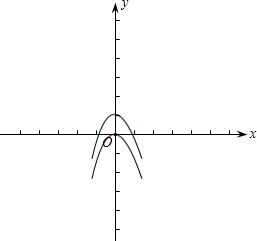
(1)抛物线y=-x2+1向下平移一个单位得到抛物线y=-x2;
(2)对于函数y=-x2+1:
①当x<0时,y随x的增大而减小;
②当x=0时,函数y有最大值,最大值是1;
③令y=-x2+1=0,
解得x=±1,
∴与x轴的交点坐标为(-1,0)(1,0),
令x=0,解得:y=1,
∴与y轴交与(0,1).
