问题
解答题
若f（x）=x2-x+b，且f（log2a）=b，log2[f（a）]=2（a≠1）。
（1）求f（log2x）的最小值及对应的x值；
（2）x取何值时，f（log2x）>f（1），且log2[f（x）]＜f（1）。
答案
解：（1）∵f（x）=x2-x+b，
∴f（log2a）=（log2a）2-log2a+b，
由已知（log2a）2-log2a+b=b，
∴log2a（log2a-1）=0
∵a≠1，
∴log2a=1，
∴a=2
又log2[f（a）]=2，
∴f（a）=4
∴a2-a+b=4，
∴b=4-a2+a=2
故f（x）=x2-x+2
从而f（log2x）=（log2x）2-log2x+2
=（log2x-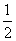
）2+
∴当log2x=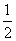
，即x=
时，f（log2x）有最小值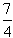
。
（2）由题意
。
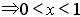