问题
解答题
已知函数f(x)=loga(x+1),g(x)=loga(4-2x)(a>0,且a≠1),
(Ⅰ)求函数f(x)-g(x)的定义域;
(Ⅱ)求使函数f(x)-g(x)的值为正数的x的取值范围.
答案
解:(Ⅰ)由题意可知,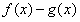
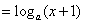
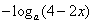 ,
,
由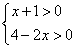 ,解得:
,解得: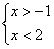 ,
,
∴-1<x<2,
∴函数的定义域是(-1,2).
(Ⅱ)由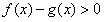 ,得
,得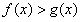 ,
,
即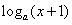
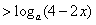 , ①
, ①
当a>1时,由①可得,x+1>4-2x,解得:x>1,
又-1<x<2,∴1<x<2;
当0<a<1时,由①可得,x+1<4-2x,解得:x<1,
又-1<x<2,∴-1<x<1;
综上所述:当a>1时,x的取值范围是(1,2);
当0<a<1时,x的取值范围是(-1,1).