问题
解答题
已知函数f(x)=loga(ax-1),(a>0且a≠1)。
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)若函数y=f(x)过(1,0)点,求f(x)的解析式,并用定义法证明函数f(x)在定义域上是增函数;
(III)在(Ⅱ)的条件下,若函数g(x)=f(x)-log2(m·2x+m)在(0,+∞)上存在零点,求实数m的取值范围。
答案
解:(Ⅰ)由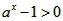 得
得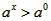 ,
,
①当a>1时,解得:x>0,此时,函数f(x)的定义域为(0,+∞),
②当0<a<1时,解得:x<0,此时,函数f(x)的定义域为(-∞,0);
(Ⅱ)由已知得f(1)=0,即 ,解得:a=2
,解得:a=2
所以,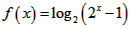 ,x>0
,x>0
设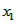 ,
, 是区间(0,+∞)上的任意两个实数,且
是区间(0,+∞)上的任意两个实数,且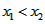 ,
,
则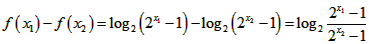 ,
,
因为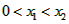 ,所以
,所以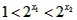 ,即
,即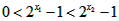 ,
,
于是得: ,所以
,所以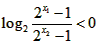
即 ,所以
,所以 ,
,
所以函数f(x)在定义域上是增函数;
(III)由(Ⅱ)得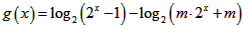 ,
,
由题意得,方程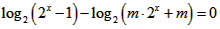 在(0,+∞)有实根,
在(0,+∞)有实根,
即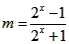 ,对
,对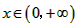 成立,
成立,
令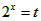 ,
,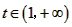 ,则
,则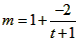 ,因为函数
,因为函数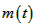 在(1,+∞)上为增函数,
在(1,+∞)上为增函数,
由函数m(t)的图象可知:m∈(0,1)
综上所述:实数m的取值范围为(0,1)
