问题
解答题
某重点大学自主招生考试过程依次为自荐材料审查、笔试、面试共三轮考核.规定:只能通过前一轮考核才能进入下一轮的考核,否则将被淘汰;三轮考核都通过才算通过该高校的自主招生考试.学生甲三轮考试通过的概率分别为
(1)求甲通过该高校自主招生考试的概率; (2)若学生甲每通过一轮考核,则家长奖励人民币1000元作为大学学习的教育基金.记学生甲得到教育基金的金额为X,求X的分布列和均值. |
答案
(1)设“学生甲通过该高校自主招生考试”为事件A,
则P(A)=
×2 3
×3 4
=4 5
,2 5
所以学生甲通过该高校自主招生考试的概率为
. …3分2 5
(2)X的可能取值为0元,1000元,2000元,3000元. …4分
P(X=0)=1-
=2 3
,…5分P(X=1000)=1 3
×(1-2 3
)=3 4
,…6分1 6
P(X=2000)=
×2 3
×3 4
=1 5
,…7分1 10
P(X=3000)=
×2 3
×3 4
=4 5
.2 5
所以,X的分布列为
| X | 0 | 1000 | 2000 | 3000 | ||||||||
| P |
|
|
|
|
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 10 |
| 2 |
| 5 |
| 4700 |
| 3 |

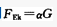 ,其中系数α与()有关。
,其中系数α与()有关。