问题
解答题
已知函数f（x）=loga（2-ax），是否存在实数a，使函数f（x）在[0，1]上是关于x的减函数，若存在，求a的取值范围。
答案
解：∵a>0，且a≠1，
∴u=2-ax在[0，1]上是关于x的减函数
又f（x）=loga（2-ax）在[0，1]上是关于x的减函数，
∴函数y=logau是关于u的增函数，且对x∈[0，1]时， u=2-ax恒为正数
其充要条件是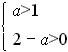
，即1＜a＜2
∴a的取值范围是（1，2）。