问题
解答题
已知lg(3x)+lgy=lg(x+y+1)。
(1)求xy的最小值;
(2)求x+y的最小值。
答案
解:由lg(3x)+lgy=lg(x+y+1),得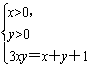
(1)∵x>0,y>0,
∴3xy=x+y+1≥2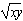 +1,
+1,
∴3xy-2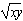 -1≥0,
-1≥0,
即3(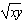 )2-2
)2-2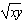 -1≥0,
-1≥0,
∴(3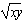 +1)(
+1)(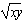 -1)≥0,
-1)≥0,
∴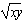 ≥1,
≥1,
∴xy≥1,
当且仅当x=y=1时,等号成立
∴xy的最小值为1。
(2)∵x>0,y>0,
∴x+y+1=3xy≤3·(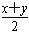 )2,
)2,
∴3(x+y)2-4(x+y)-4≥0,
∴[3(x+y)+2][(x+y)-2]≥0,
∴x+y≥2,当且仅当x=y=1时取等号,
∴x+y的最小值为2。
