问题
解答题
已知函数y=g（x）与f（x）=loga（x+1）（a＞1）的图象关于原点对称．
（1）写出y=g（x）的解析式；
（2）若函数F（x）=f（x）+g（x）+m为奇函数，试确定实数m的值；
（3）当x∈[0，1）时，总有f（x）+g（x）≥n成立，求实数n的取值范围．
答案
解：（1）设M（x，y）是函数y=g（x）图象上任意一点，
则M（x，y）关于原点的对称点为N（﹣x，﹣y）
N在函数f（x）=loga（x+1）的图象上，
∴﹣y=loga（﹣x+1）
（2）∵F（x）=loga（x+1）﹣loga（1﹣x）+m为奇函数．
∴F（﹣x）=﹣F（x）
∴loga（1﹣x）﹣loga（1+x）+m=﹣loga（1+x）+loga（1﹣x）﹣m ∴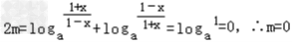 
（
3）由 
设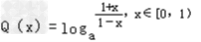
，由题意知，只要Q（x）min≥n即可 ∵
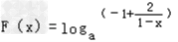在[0，1）上是增函数
∴n≤0