问题
填空题
在Rt△ABC中，∠ACB=90°，CD⊥AB于点D．已知AC=
|
答案
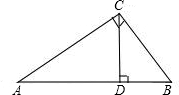
在直角△ABC中，根据勾股定理可得：AB=
=AC2+BC2
=3．(
)2+225
∵∠B+∠BCD=90°，∠ACD+∠BCD=90°，
∴∠B=∠ACD．
∴sin∠ACD=sin∠B=
=AC AB
．5 3
搜题请搜索小程序“爱下问搜题”
在Rt△ABC中，∠ACB=90°，CD⊥AB于点D．已知AC=
|
在直角△ABC中，根据勾股定理可得：AB=
=AC2+BC2
=3．(
)2+225
∵∠B+∠BCD=90°，∠ACD+∠BCD=90°，
∴∠B=∠ACD．
∴sin∠ACD=sin∠B=
=AC AB
．5 3