问题
解答题
已知f（x）=lg（x+1）
（1）若0＜f（1-2x）-f（x）＜1，求x的取值范围；
（2）若g（x）是以2为周期的偶函数，且当0≤x≤1时，g（x）=f（x），求函数y=g（x）（x∈[1，2]）的反函数。
答案
解：（1）由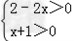
解得：-1＜x＜1
由0＜lg（2-2x）-lg（x+1）=lg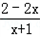
＜1
得：1＜
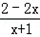＜10，
∵x+1＞0，
∴x+1＜2-2x＜10x+10，
∴
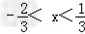
由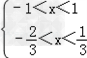
得：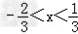
。
（2）当x∈[1，2]时，2-x∈[0，1]，
∴y=g（x）=g（x-2）=g（2-x）=f（2-x）=lg（3-x），
由单调性可知y∈[0，lg2]，
又∵x=3-10y，
∴所求反函数是y=3-10x，x∈[0，lg2]。