问题
填空题
若直角梯形的两腰之比为1：2，该梯形的最大内角的度数是______．
答案
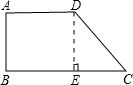
作DE⊥BC于点E，可得矩形ABED和直角三角形DEC，
∴DE=AB，
∠ADE=90°，
∵AB：CD=1：2；
∴cos∠CDE=DE：DC=1：2，
∴∠CDE=60°，
∴∠ADC=90°+60°=150°，
故答案为150°．
搜题请搜索小程序“爱下问搜题”
若直角梯形的两腰之比为1：2，该梯形的最大内角的度数是______．
作DE⊥BC于点E，可得矩形ABED和直角三角形DEC，
∴DE=AB，
∠ADE=90°，
∵AB：CD=1：2；
∴cos∠CDE=DE：DC=1：2，
∴∠CDE=60°，
∴∠ADC=90°+60°=150°，
故答案为150°．