问题
填空题
四边形ABCD中，AD∥BC，已知BC=CD=AC=2
|
答案
以C为圆心BC为半径，作⊙C．延长BC交⊙C与点B′，连接DB′．
则∠BDB′=90°．
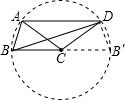
∵AD∥BC，
∴DB′=AB=
，6
又∵BB′=2BC=4
，3
由勾股定理得BD=
．42
搜题请搜索小程序“爱下问搜题”
四边形ABCD中，AD∥BC，已知BC=CD=AC=2
|
以C为圆心BC为半径，作⊙C．延长BC交⊙C与点B′，连接DB′．
则∠BDB′=90°．
∵AD∥BC，
∴DB′=AB=
，6
又∵BB′=2BC=4
，3
由勾股定理得BD=
．42