问题
解答题
袋中装有大小相同的2个白球和3个黑球.
(Ⅰ)采取放回抽样方式,从中依次摸出两个球,求两球颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中依次摸出两个球,记ξ为摸出两球中白球的个数,求ξ的期望和方差.
答案
(Ⅰ)记“摸出一球,放回后再摸出一个球,两球颜色不同”为事件A,
摸出一球得白球的概率为
,2 5
摸出一球得黑球的概率为
,3 5
由互斥事件和相互独立事件的概率公式得到
∴P(A)=
×2 5
+3 5
×3 5
=2 5
.12 25
(Ⅱ)由题意知ξ可取0,1,2,
∵当ξ=0时,表示摸出两球中白球的个数为0,
当ξ=1时,表示摸出两球中白球的个数为1,
当ξ=2时,表示摸出两球中白球的个数为2,
∴依题意得P(ξ=0)=
×3 5
=2 4
,P(ξ=1)=3 10
×3 5
+2 4
×2 5
=3 4
,P(ξ=2)=3 5
×2 5
=1 4
,1 10
∴Eξ=0×
+1×3 10
+2×3 5
=1 10
,4 5
Dξ=(0-
)2×4 5
+(1-3 10
)2×4 5
+(2-3 5
)2×4 5
=1 10
.9 25
即摸出白球个数ξ的期望和方差分别是
,4 5
.9 25

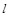 的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹300角且绷紧,小球A处于静止,对小球施加的最小力F=___________
的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹300角且绷紧,小球A处于静止,对小球施加的最小力F=___________