问题
解答题
甲口袋中装有两个相同的小球,它们分别写有1和2;乙口袋中装有三个相同的小球,它们分别写有3、4和5;丙口袋中装有两个相同的小球,它们分别写有6和7,从这3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有两个偶数的概率是多少?
(2)取出的3个小球上全是奇数的概率是多少?
答案
解:根据题意,画出如下的“树形图”:

从树形图中可以看出,所有可能出现的结果共有12个;
(1)取出的3个小球上恰好有两个偶数的结果有4个,即1,4, 6;2,3,6;2,4,7;2,5,6,
所以P(两个偶数)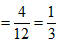 ;
;
(2)取出的3个小球上全是奇数的结果有2个,即1,3,7;1,5.7,
所以P(三个奇数) 。
。
