问题
选择题
设集合A={x|x2+2x-3>0},集合B={x|x2-ax-1≤0,a>0},若A∩B中恰含有一个整数,则实数a的取值范围是( )
|
答案
A={x|x2+2x-3>0}={x|x>1或x<-3},
设f(x)=x2-ax-1,则f(0)=-1<0,对称轴x=-
=-a 2
>0,a 2 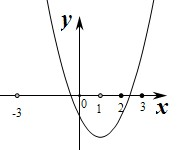
∴要使A∩B中恰含有一个整数,
则
,f(2)≤0 f(3)>0
即
,4-2a-1≤0 9-3a-1>0
∴
,即a≥ 3 2 a< 8 3
≤a<3 2
,8 3
∴实数a的取值范围是[
,3 2
).8 3
故选:B
