问题
填空题
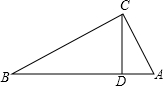
在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BD=6,则sinA=______.
答案
由题意知,△ADC∽△CDB,
∴CD:AD=BD:CD.
设AD=x,∴CD=
.6x
在Rt△ADC中,
AC2=AD2+CD2,
∴6x+x2=16,
解得x=2(负值舍去),
∴CD=2
,3
∴sinA=
=CD AC
.3 2
在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BD=6,则sinA=______.
由题意知,△ADC∽△CDB,
∴CD:AD=BD:CD.

设AD=x,∴CD=
.6x
在Rt△ADC中,
AC2=AD2+CD2,
∴6x+x2=16,
解得x=2(负值舍去),
∴CD=2
,3
∴sinA=
=CD AC
.3 2