问题
计算题
如果公路上有一列汽车车队以15 m/s的速度正在匀速行驶，相邻车间距为20 m，后面有一辆摩托车以25 m/s的速度同向行驶，当它距离车队最后一辆车20m时刹车，以0.5 m/s2的加速度做匀减速运动，摩托车在车队旁边行驶而过，设车队车辆数足够多，求：
（1）摩托车最多能与车队中的几辆汽车相遇？
（2）摩托车从赶上车队到离开车队，共经历多长时间？
答案
解：（1）设摩托车与某一辆汽车速度相同时需要时间t
则有V1=V2－at， 得：t=20s
在此段时间内摩托车前行距离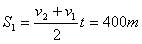
汽车前行距离S2=V1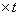
=300m
摩托车相遇的汽车数为N=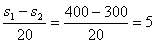
辆
（2）设摩托车与相距最近的汽车相遇需要的时间为t
则有位移关系：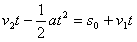
代入数据，化简得：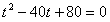
， 解得：
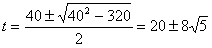s
即第一次与最后一辆相遇时间为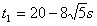
第二次与最后一辆相遇时间为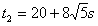
第二次与最后一辆相遇时摩托车速度为
即摩托车离开车队时，摩托车没有停止
所以摩托车经历的时间