问题
选择题
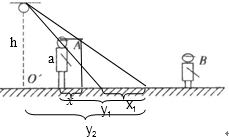
夜晚有两个高矮不同的小朋友A和B,A比B高,相距d.他们分别站在路灯下,O′点是路灯在地面上的投影.A、B两人的连线通过O′点,如图所示.他们头部分别在地面上留下两个影子A′和B′,相距d′,当两人沿过O′点的直线,以相同的速度行进时.A′和B′的距离将( )
A.不断增大
B.不断减小
C.先增大,后减小
D.先减小,后增大
答案
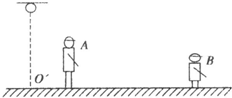
如图所示:
设A小朋友身高为a,灯高度为h,若A小朋友向前移动x,则影子向前移动x1,由相似三角形的性质可得
=a h
=y1-x1 y2-x1 y1-x y2
=y1 y2
,解得′由两个影子A′和B′,相距d′,以相同的速度行进时,y1-x-x1 y2+x
A小朋友影子与原影子的距离x1′=
,B小朋友影子与原影子的距离x1″=hx h-a
,hx h-b
因为x1′>x1″,A比B高,即a>b,
此时影子d″=d′-x1′+x1″<d′.
同理,当两人头部的影子达到重合后,再继续远离路灯时,
因为A比B高,即a>b,
此时A影子会超过B的影子,
两者的距离变化为:先减小,后增大.
故选D.