问题
解答题
已知等腰三角形的两边长分别为2和4，求这个三角形底角的余弦函数值和正切函数值．
答案
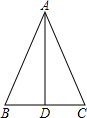
如图，在△ABC中，∵等腰三角形边长为2和4，
则腰长AB=AC=4，CB=2，
过顶点A作底边的高AD，
根据勾股定理得到高AD=
，15
可得底角的余弦值为
，1 4
正切函数值为
，15
当腰长是2，底边是4时，不满足三边关系定理，
总之，可得底角的余弦值为
，正切函数值为1 4
．15
搜题请搜索小程序“爱下问搜题”