问题
填空题
设f(x)=|lgx|,若a≠b,且f(a)=f(b),则a•b=______.
答案
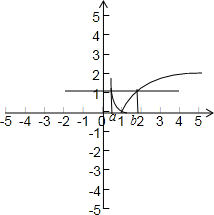
因为a≠b,不妨设a<b,如图所示:则0<a<1,b>1,
由f(a)=f(b),得|lga|=|lgb|,即-lga=lgb,所以lga+lgb=0,lgab=0,所以ab=1.
故答案为:1.
设f(x)=|lgx|,若a≠b,且f(a)=f(b),则a•b=______.
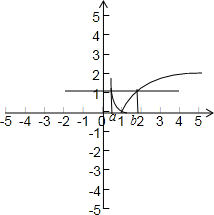
因为a≠b,不妨设a<b,如图所示:则0<a<1,b>1,
由f(a)=f(b),得|lga|=|lgb|,即-lga=lgb,所以lga+lgb=0,lgab=0,所以ab=1.
故答案为:1.