设定义域为r的函数f（x）=|lgx|x＞0-x2-2xx≤0，若关于x的函数y

问题选择题

设定义域为r的函数f（x）=

|lgx| x＞0

-x2-2x x≤0

，若关于x的函数y=2f²（x）+2bf（x）+1有8个不同的零点，则实数b的取值范围是（　　）

A．-

＜b＜

B．-

＜b＜-

C．-2＜b＜-

D．-

＜b＜-

或b＞

答案

令t=f（x），则原函数等价为y=2t²+2bt+1．做出函数f（x）的图象如图：

，

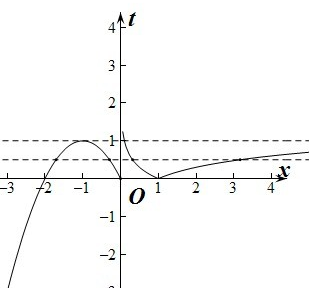
图象可知当由0＜t＜1时，函数t=f（x）有四个交点．

所以要使关于x的函数y=2f²（x）+2bf（x）+1有8个不同的零点，则函数y=2t²+2bt+1有两个根t₁，t₂，

且0＜t₁＜1，0＜t₂＜1．

令g（t）=2t²+2bt+1，则由根的分布可得

△＞0

g(0)＞0

g(1)＞0

0＜-

2×2

＜1

，即

△=4b2-8＞0

g(0)=1＞0

g(1)=2b+3＞0

-2＜b＜0

，

解得

b＞

或b＜-

b＞-

-2＜b＜0

，即-

＜b＜-

，所以实数b的取值范围是-

＜b＜-

．

故选B．