问题
计算题
A、B两列火车在同一轨道上同向行驶，A车在前，速度vA=10 m/s，B车在后，速度vB=30 m/s。因能见度低，B 车在距A车500 m时才发现前方有A车，这时B车立即刹车，但要经过1 800 m车才能停下，问：
（1）A车若仍按原速度前进，两车是否会相撞？若会相撞，将在何时何地发生？
（2）B车在刹车的同时发出信号，A车司机在收到信号1.5s后加速前进，则A车的加速度多大时，才能避免发生事故？
答案
解：（1）B车刹车时加速度大小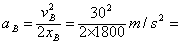
0.25 m/s2
B车停下来的运动时间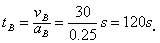
设B车刹车后经时间t两车速度相等，即vB-aBt=vA，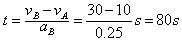
此时A车前进距离xA'=vAt=10×80m=800 m
B车前进距离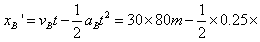
802 m=1 600 m
因xA'+500 m=1 300 m＜xB'，故两车相撞
设两车相撞时经历时间为t'，则有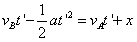
即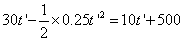
，解得t'≈31.01 s（另一根不合题意，舍去）
设相撞处距B车开始刹车处距离为xB''
则xB''=vAt'+x=10×31.01m+500 m=810.1 m
（2）设B车恰好不与A车相撞时，A车的加速度为aA，当B车追上A车时，两车速度相等，此时距B车开始刹车的时间为t0
故有xA+x=xB，即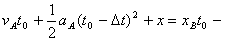
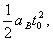①
且vB-aBt0=vA+aA（t0-△t)，即30-0.25t0=10+ aA（t0-1.5） ②
解①②两式得t0≈49.43 s，aA≈0.16 m/s2
故当A车的加速度大于0.16 m/s2时，可避免两车相撞