问题
填空题
将等腰△ABC绕着底边BC的中点M旋转30°后，如果点B恰好落在原△ABC的边AB上，那么∠A的余切值等于 ▲ ．
答案
由△ABC绕点M旋转30°得到△A′B′C′，根据旋转的性质得到MB=MB′，∠BMB′=30°，根据等腰三角形的性质计算出∠B=由△ABC绕点M旋转30°得到△A′B′C′，根据旋转的性质得到MB=MB′，∠BMB′=30°，根据等腰三角形的性质计算出∠B=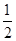
（180°-30°）=75°，则∠A=180°-75°-75°=30°，再根据余切的定义即可得到∠A的余切值．
解：如图，
∵△ABC绕点M旋转30°得到△A′B′C′，
∴MB=MB′，∠BMB′=30°，
∴∠B=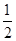（180°-30°）=75°，
∵AB=AC，
∴∠B=∠C=75°，
∴∠A=180°-75°-75°=30°，
∴∠A的余切值为
．
故答案为
