问题
填空题
Rt△ABC中，∠A=900，BC=4,有一个内角为600，点P是直线AB上不同于A、B的一点，且∠ACP=300，则PB的长为 ．
答案
4或
或
。
分两种情况考虑：
当∠ABC=60°时，如图所示：
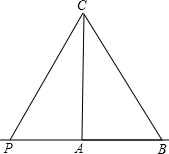
∵∠CAB=90°，∴∠BCA=30°。
又∵∠PCA=30°，∴∠PCB=∠PCA+∠ACB=60°。
又∵∠ABC=60°，∴△PCB为等边三角形。
又∵BC=4，∴PB=4。
当∠ABC=30°时，
（i）当P在A的右边时，如图所示：
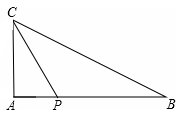
∵∠PCA=30°，∠ACB=60°，∴∠PCB=90°。
又∠B=30°，BC=4，
∴
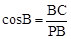，即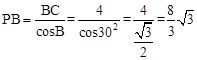
。
（ii）当P在A的左边时，如图所示：
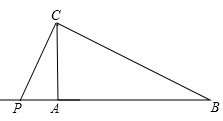
∵∠PCA=30°，∠ACB=60°，∴∠BCP=30°。
又∠B=30°，∴∠BCP=∠B。∴CP=BP。
在Rt△ABC中，∠B=30°，BC=4，∴AC=
BC=2。
根据勾股定理得：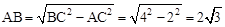
，
∴AP=AB－PB=
－PB。
在Rt△APC中，根据勾股定理得：AC2＋AP2=CP2=BP2，即22+（－PB）2=BP2，
解得：BP=。
综上所述，BP的长为4或或。