问题
解答题
在区间［-1，1］上任取两数a、b，求二次方程x2+ax+b=0的两根
(1)都是实数的概率；
(2)都是正数的概率.
答案
(1) 概率为
(N为总数组数)=0.54
(2) 概率为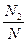
=0.021.
根据两根满足的条件得到a、b满足的关系，利用随机模拟求得概率.
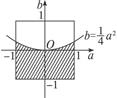
据题意-1≤a≤1，-1≤b≤1，以a为横坐标、b为纵坐标，得到一个边长为2的正方形.
(1)若a、b都是实数，则Δ=a2-4b≥0，即b≤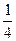
a2，利用随机模拟求概率.
(ⅰ)利用计算机或计算器产生0至1区间的两组随机数，a1=RAND，b1=RAND；
(ⅱ)经平移和伸缩变换，a=a1*2-1，b=b1*2-1；
(ⅲ)数出满足b≤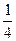a2的数组数N1.
则所求概率为(N为总数组数)=0.54.
(2)若两根都是正数，则有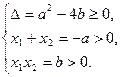
即b≤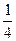a2且a＜0，b＞0.
在第(1)问求出的随机数中数出满足b≤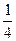a2且a<0，b>0的数组数N2，则所求概率为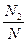=0.021.