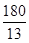
连接AC

∵ AM垂直BC，AB=13，BM=5

∴ AM=12

∵ AM垂直BC，MC=9，AM=12

∴ AC=15

∵ AM垂直BC，AN垂直CD

∴∠AMC+∠ANC=90+90=180度

∴ AMCN四点共圆

∴∠MNC=∠MAC

∵ AC=15，MC=9，AM垂直BC

∴ sin(∠MNC)=sin(∠MAC)=MC/AC=3/5

∵在平行四边形ABCD中 DC//AB

∴∠MCN=180-∠ABM

∴ sin(∠MCN)=sin(∠ABM)

∵ AB=13，AM=12，AM垂直BC

∴ sin(∠MCN)=sin(∠ABM)=AM/AB=12/13

∵在三角形MCN中由正弦定理有 MN/sin(∠MCN)=MC/sin(∠MNC)

∵sin(∠MCN=12/13，MC=9，sin(∠MNC)=3/5

∴ MN=180/13