问题
计算题
一汽车从静止开始以3m/s2的加速度行驶,恰有一自行车以6 m/s的速度从汽车旁边匀速驶过。
(1)汽车从开动后在追上自行车之前经多长时间两者相距最远?此时距离是多少?
(2)什么时候追上自行车,此时汽车的速度是多少?
答案
解法一:解析法
(1)汽车从开动后速度由零逐渐增大,而自行车速度是定值,当汽车的速度还小于自行车的速度时,两者距离越来越大,当汽车的速度大于自行车的速度时,两者距离越来越小。所以当两车的速度相等时,两车之间距离最大
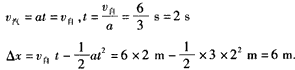
(2)汽车追上自行车时,两车位移相等
v自t'=-1/2at'2,代入数值得t'=4 s,v'汽=at'=3×4 m/s=12 m/s
解法二:图象法
如图所示,作出v-t图
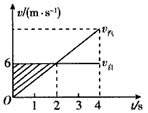
(1)设相遇前t秒两车速度相等,v汽=at =6 m/s,即3t=6 m/s
解得t=2 s时两车相距最远,两车的位移差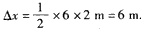
(2)由图知,t=2s以后,若两车位移相等,即v-t图象与时间轴所夹的面积相等,由几何关系知,相遇时间为t'=4 s,此时v汽=2v自=12 m/s