问题
选择题
如图,绝缘光滑的圆环竖直放置在水平向右的匀强电场中,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,从a点由静止释放,沿abc运动到d点时的速度恰好为零。在a→b→c→d的过程中,小球
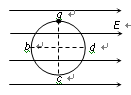
A.在b点的向心加速度最大
B.在b点的机械能最大
C.在d点的电势能最大
D.在d点的加速度为零
答案
BC
本题考查电场力做功;功能原理的应用;电势能;向心加速度与加速度。解答本题关键是根据电场力做功判断电势能的变化,根据除重力外的其它力做功判断机械能的变化,难点在于运用类比的方法确定速度最大的位置。
A、设小球从a到d过程中,重力做功为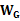 ,克服电场力做功为
,克服电场力做功为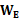 ,由动能定理得,
,由动能定理得,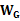 -
-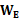 =0,则有
=0,则有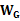 =
=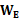 ,小球从a到c过程中,重力做功为2
,小球从a到c过程中,重力做功为2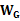 ,电场力做功为零,则由动能定理得,小球经过c点的动能
,电场力做功为零,则由动能定理得,小球经过c点的动能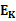 =2
=2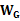 ,小球从a到b过程中,重力做功为
,小球从a到b过程中,重力做功为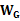 ,电场力做功为
,电场力做功为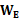 ,则由动能定理得,小球经过b点的动能
,则由动能定理得,小球经过b点的动能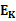 =2
=2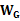 ,可见,bc中点类似于单摆的平衡位置,小球经中点时速度最大,由
,可见,bc中点类似于单摆的平衡位置,小球经中点时速度最大,由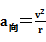 知,小球经bc中点时向心加速度最大,故A错误;
知,小球经bc中点时向心加速度最大,故A错误;
B、小球从a运动到b的过程中,电场力做正功最多,根据功能关系可知,小球在b点时的机械能最大,故B正确;
C、小球从a运动到d的过程中,电场力做负功最多,小球在d点时的电势能最大,故C正确;
D、小球到达d点的速度为零,向心加速度为零,向心力为零,小球还受到竖直向下的重力,加速度方向竖直向下,加速度不为零,故D错误。
因此选BC
