2或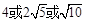

题目分析：分情况讨论，①以A为直角顶点，向外作等腰直角三角形DAC；②以C为直角顶点，向外作等腰直角三角形ACD；③以AC为斜边，向外作等腰直角三角形ADC．分别画图，并求出BD．

①以A为直角顶点，向外作等腰直角三角形DAC，

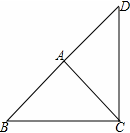
∵∠DAC=90°，且AD=AC，

∴BD=BA+AD=2+2=4；

②以C为直角顶点，向外作等腰直角三角形ACD，连接BD，过点D作DE⊥BC，交BC的延长线于E．

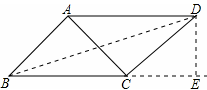
∵△ABC是等腰直角三角形，∠ACD=90°，

∴∠DCE=45°，

又∵DE⊥CE，

∴∠DEC=90°，

∴∠CDE=45°，

∴，

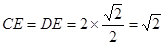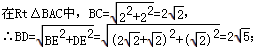
③以AC为斜边，向外作等腰直角三角形ADC，

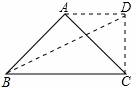
∵∠ADC=90°，AD=DC，且AC=2，

又∵△ABC、△ADC是等腰直角三角形，

∴∠ACB=∠ACD=45°，

∴∠BCD=90°，

当BD=2，这时△ABC与△BCD为正方形，

故BD的长等于2或．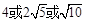

点评：本题综合性强，难度较大，是中考常见题，一般出现于选择、填空的最后一题.