问题
选择题
等腰三角形的底角为30°,底边长为2
|
答案
作AD⊥BC于D点.
∵△ABC是等腰三角形,AD⊥BC,∠B=30°,
∴BD=CD=
BC=1 2
×21 2
=3
.3
∵cos∠B=cos30°=
=BD AB
=3 AB
,3 2
∴AB=2.
故选C.
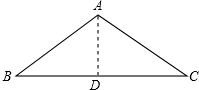
等腰三角形的底角为30°,底边长为2
|
作AD⊥BC于D点.
∵△ABC是等腰三角形,AD⊥BC,∠B=30°,
∴BD=CD=
BC=1 2
×21 2
=3
.3
∵cos∠B=cos30°=
=BD AB
=3 AB
,3 2
∴AB=2.
故选C.
