(本小题满分12分)
有三种产品,合格率分别为0.90,0.95和0.95,各抽取一件进行检验.
(1)求恰有一件不合格的概率;
(2)求至少有两件不合格的概率.(精确到0.001)
解:设三种产品各抽取一件,抽到合格产品的事件分别为A,B和C。
(1)P(A)=0.90,P(B)=0.95, P(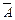 )=0.10,P(
)=0.10,P(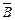 )=0.05.
)=0.05.
因为事件A,B,C相互独立,恰有一件不合格的概率为
P(AB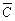 )+P(A
)+P(A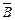 C) +P(
C) +P(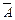 BC)
BC)
=P(A)·P(B) ·P(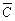 )+P(A)·P(
)+P(A)·P(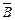 )·P(C) +P(
)·P(C) +P(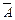 )·P(B) ·P(C)
)·P(B) ·P(C)
=2×0.90×0.95×0.05+0.10×0.95××0.95≈0.176
即恰有一件不合格的概率为0.176.…………………………………………6分
(2)解法一:至少有两件不合格的概率为
P(A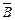
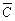 )+P(
)+P(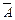 B
B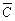 ) +P(
) +P(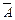
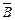 C) +P(
C) +P(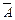
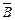
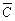 )
)
=0.90×0.052+2×0.10×0.05×0.95+0.10×0.052=0.012,
即至少有两件不合格的概率为0.012.…………………………………………12分
解法二 三件产品都合格的概率为
P(ABC) =P(A)·P(B)·P(C) =0.90×0.952≈0.812.
由(1)知,恰有一件不合格的概率为0.176,所以至少有两件不合格的概率为
1- [P(ABC) +0.176] =1-(0.812+0.176)=0.012.……………………12分
