问题
问答题
设(1)f(x)在[a，b](a＞0)上有连续的非负导数，且f(a)=1；(2)对任意x∈[a，b]，在曲线y=f(x)上从a到x这一段的弧长
求由x=a，x=b，y=0及y=f(x)所围图形绕x轴旋转的旋转体体积．
答案
参考答案：
先由弧长的关系式求出f(x)的表示式，再由旋转体的计算公式求出其图形绕x轴旋转的旋转体体积．
先求出f(x)的表示式．由曲线弧长公式，有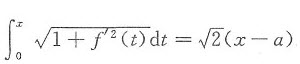
将上式两边对x求导，得到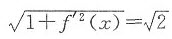
，即f’2(x)=1．
因而f’(x)=1(舍去f’(x)=-1，因题设f’(x)≥0)，解得
f(x)=x+c．
将f(a)=1代入上式得c=1-a，因而
f(x)=x+1-a．
故所求旋转体体积为