问题
填空题
设A,B均为三阶方阵,λ1=1,λ2=2,λ3=-2为A的三个特征值,|B|=-3,则行列式|2A*B+B|=()。
答案
参考答案:|2A*B+B|=|(2A*+E)B|=|2A*+E||B|=105×(-3)=-315.
解析:
利用矩阵行列式等于其特征值之积的结论求之.
由题设知|A|=λ1λ2λ3=-4,A*的特征值分别为
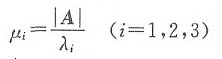
则μ1=4, μ2=-2,μ3=2.
而矩阵2A+E的特征值为2μi+1,即-7,-3,5,故行列式
|2A*+E|=(-7)×(-3)×5=105,
从而行列式
|2A*B+B|=|(2A*+E)B|=|2A*+E||B|=105×(-3)=-315.
