问题
问答题
已知A,B为三阶矩阵,且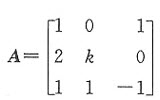
秩(B)=2,秩(AB)=1.
试求AX=0的通解.
答案
参考答案:
先确定A的秩,再确定待定元素k,最后用基础解系的简便求法求出其基础解系.
因秩(B)=2,秩(AB)=1,则秩(A)为不可逆矩阵.这是因为:如果A为可逆矩阵,则
秩(AB)=秩(B)=2
这与秩(AB)=1矛盾,故
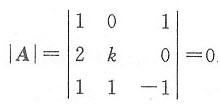
再由三阶行列式的对角线求法即得
|A|=k+2+0-k-0-0=-2k+2=0。
故k=1.对A施行初等行变换,将A化为含最高阶的单位矩阵的矩阵:

则AX=0的基础解系只含一个解向量
α=[-1,2,1]T,
其通解为kα,其中k为任意常数.
